What if I skip df[intercept]= 1 in linear regression?
Linear regression is a primary type of predictive analysis where we are trying to find the best-fitted line for a scatter plot, and for simple linear regression this line is represented as:
$$ \hat{y}= b1x+b0 $$
where, b1 is the slope and b0 is the intercept
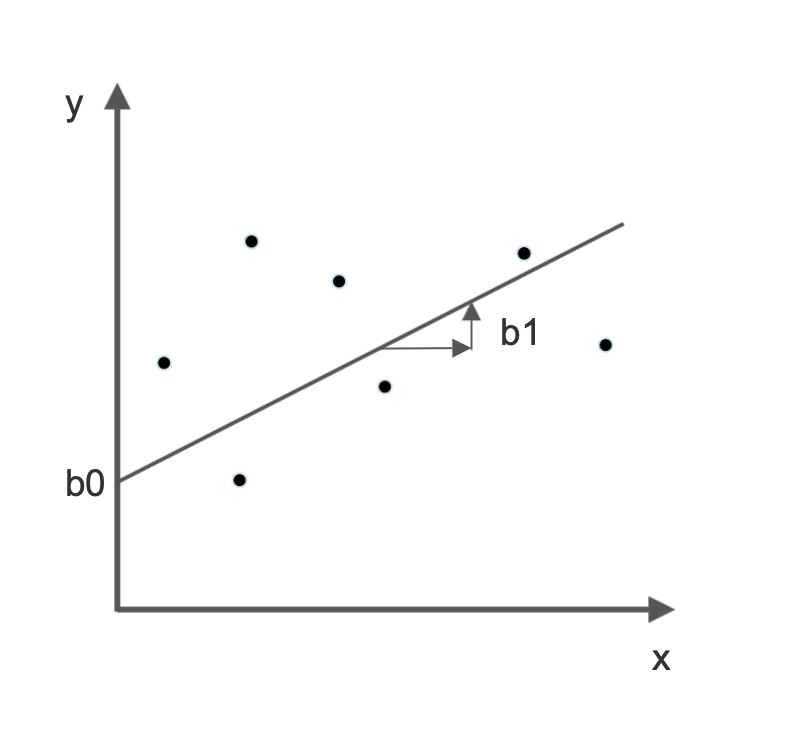
Let's take an example where we want to predict the price of a house based on how many bedrooms it has. The variable we want to predict is the price, which is represented by y and x means the no.of bedrooms in the house. In this context, the change in price, when we add one more bedroom to the house, is represented by value b1 and our intercept b0 is the value of the house when it has no bedrooms at all (you can crash in the bathtub). Now that we have our interpretations down let's dive into some code.
To find the value of the parameters b1 and b0 of the best-fitted line, we write a simple three-line code in python.
df['intercept'] = 1 # df is dataframe containing our data
#performing linear regression
linear_model=sm.OLS(df['Price'],df[['intercept','bedrooms']]) #y:price, x:[intercept,bedrooms]
results = linear_model.fit()
results.summary()
In the code snippet above, notice how we added a column 'intercept' to our data before performing linear regression and set its value to 1. This line of code, begets the question - what if I skip this line of code or have intercept value other than 1?
In the linear regression model, OLS finds "weight * predictor" for each term used in the regression. So, if we skip the intercept variable, which looks like this:
linear_model = sm.OLS(df['price'],df['bedrooms']) # y:price, x:bedrooms
then, OLS will see the equation as:
$$y = b1*x$$
OLS algorithm will now proceed to find b1 and leave out b0 because there is only one predictor x given to it for which it will calculate the weight b1. Without the intercept, we force the line to always pass by the origin (0, 0) and we never get the predictive relationship between price and the no.of bedrooms that we are seeking as per our fitted model. There are rare cases where we skip the intercept but it only when by some theoretical or some other reason we have a guarantee the line passes through the origin.
We are now clear we want the value for the intercept b0; therefore, we add a column for it in our database. For our OLS equation to be complete, we need a predictor for the weight = b0. Since we want the value of intercept unaltered, we multiply it by 1, that is, weight(=b0) * predictor(=1). As a result, our OLS equation is:
$$y = b1*x + b0*1$$
Now, our linear regression model knows it has to find the value of both b1 and b0.
Note: In R language, intercept is included anyway without initialization.